Banca Electrónica. Nuevos Vectores de Ataque.
(ANEXO I)
TARJETAS DE COORDENADAS
06 de Septiembre de 2006
Hugo Vázquez Caramés
hvazquez@pentest.es
Introducción
El 21 de Junio de 2006
PENTEST publicó un informe titulado "Banca Electrónica. Nuevos Vectores de Ataque" en el que se ofrecía una explicación de una serie de vectores de ataque a los sistemas de autentificación de banca on-line.
El informe demostraba como incluso los sistemas más robustos -como por ejemplo los sistemas basados en tokens- podían verse comprometidos debido a fallos en las aplicaciones web -inyección de código, etc.- en determinados puntos "estratégicos" del portal de banca.
El cambio del mecanismo de validación de usuarios en un sistema tan complejo como es la web de un banco no es tarea fácil, y por ello, el paso a sistemas más seguros se irá produciendo de manera paulatina y siempre buscando el equilibrio entre la funcionalidad y la seguridad.
Es muy difícil implementar un sistema realmente efectivo y de bajo impacto en una población que está acostumbrada al uso de contraseñas estáticas desde el origen de los ordenadores, o mejor dicho, desde el origen de los sistemas de control de accesos de dominio público.
Los tiempos avanzan y las entidades bancarias en un importante esfuerzo por ponerse al día y ofrecer el mejor de sus servicios adecuan sus sistemas de seguridad a los "nuevos tiempos".
Ya a casi nadie le cabe duda de que las contraseñas estáticas no son seguras. Todo el mundo tiene presente que todo aquel que conozca la contraseña, tiene pleno derecho de acceso al sistema que protege.
Con el fin de mitigar parte de este desagradable efecto de inseguridad, muchas entidades han puesto en marcha -algunas llevan años usándolos- unos sistemas de autentificación que basan su seguridad en unas tarjetas conocidas como "Tarjetas de Coordenadas".
Una tarjeta de coordenadas es una tabla -normalmente de las dimensiones de una tarjeta de crédito- con un conjunto de claves. Los sistemas que utilizan este método de protección, obligan a sus usuarios a introducir una de esas claves para cada transacción que desean realizar.
La seguridad de este procedimiento radica en que aunque un intruso sea capaz de "ver" una de esas claves, no es probable que pueda utilizarla para una operación no autorizada. ¿Porqué? Un razonamiento rápido lleva a la siguiente conclusión: porque la tarjeta contiene muchas claves, normalmente unas 60.
El porqué de las tarjetas
Una tarjeta "típica" tiene unas 60 claves.
Se nos plantea una pregunta: ¿La tarjeta es válida para siempre?
Porque si es así, parece que, a la larga, se "repetirán" contraseñas, es decir que para dos transacciones distintas se pedirá la misma contraseña. Y no hace falta esperar mucho. Para una tarjeta de "N" claves, este suceso se produce, como mucho a partir de "N" transacciones. Alguien puede empezar a hacer cuentas: 60 claves,... varias transacciones por mes,... o por semana,... o incluso al día... está claro que las claves inexorablemente empezarán a repetirse antes o después. Obviamente, antes, cuantas más transacciones se realicen.
¿Entonces porqué usar este sistema?
Hay que entender que el uso de tarjetas de coordenadas no es un capricho del sector de la banca. La banca conoce perfectamente este tipo de riesgos, tiene analistas, programadores y gerentes que se encargan de velar por la seguridad de sus sistemas. Actualmente existen sistemas mucho más seguros que las tarjetas de coordenadas, pero su coste y muchas veces el impacto social impiden su introducción inmediata en el mercado.
Las tarjetas de coordenadas son una solución a caballo entre los llamados sistemas OTP (One Time Password) y las contraseñas estáticas. Los sistemas OTP se caracterizan porque nunca reutilizan una contraseña. En ese sentido se puede afirmar que son bastante robustos, ya que su seguridad radica en el hecho de que, aunque un intruso sea capaz de capturar una contraseña, jamás debería de poder reutilizarla. El inconveniente es que es necesario ir suministrando contraseñas al usuario a medida que éste las va "consumiendo". Está claro que no es un sistema cómodo para el usuario de a pié, y menos para aquel que realiza muchas operaciones. Aquí es donde las tarjetas de coordenadas cobran protagonismo, pues aun sin ser sistemas OTP ofrecen una seguridad añadida al clásico mecanismo de la contraseña estática, sin repercusión económica apreciable ni impacto social.
Esta realidad ha permitido que las tarjetas se hayan extendido como un sistema de autentificación bastante común. Parece la relación perfecta entre coste, funcionalidad y seguridad.
La pregunta: ¿Son seguras?
Volvamos a analizar el motivo de la aparición de las tarjetas de coordenadas. Como se ha comentado anteriormente las tarjetas de coordenadas se diseñaron para aumentar la seguridad de las contraseñas. Las contraseñas estáticas son muy vulnerables ante distintos tipos de ataque: phishing, programas troyano que capturan pulsaciones o incluso la pantalla. Cuando un intruso consigue una contraseña estática, el "juego" ha finalizado. Con las tarjetas de coordenadas la cosa cambia. Está claro que el riesgo disminuye, no en vano existen "N" (60) contraseñas, luego parece poco probable que un intruso pueda obtener un beneficio directo con la captura de una de esas contraseñas.
Debería de ser así, pues el modelo teórico así lo establece. Desgraciadamente, y según se desprende de un estudio de campo que se ha realizado, en la mayoría de casos, pequeños descuidos a la hora de implementar este esquema permite que los sistemas de autentificación basados en tarjetas de coordenadas puedan verse vulnerados con un 100% de éxito precisamente en aquellas situaciones donde éste sistema debiera demostrar su eficacia.
Razonamiento planteado:
- un sistema de seguridad "Nuevo" se emplea como sustituto de otro sistema de seguridad "Antiguo", para proteger de un problema conocido "X".
- el sistema "Antiguo" es vulnerable a "X"
- el sistema "Nuevo" en teoría no es vulnerable a "X"
Si el sistema "Nuevo" acabara siendo vulnerable a "X" ¿Qué sucedería?
En este punto se plantean varias líneas de pensamiento. Habrá quien opine, que en el peor de los casos, simplemente se estaría como antes, es decir, como cuando se usaba el sistema "Antiguo", que era vulnerable a "X". No hay mejora, pero tampoco hay empeoramiento de la situación... ¿Seguro?
Nuestra línea de pensamiento analiza el problema desde otro punto de vista.
- el sistema "Nuevo" se adoptó para paliar una debilidad "X" muy conocida.
- el sistema "Nuevo", amparándose en esta nueva seguridad, le ofrece al usuario la posibilidad de operar en entornos en los que antes, cuando se usaba el sistema "Antiguo", dicho usuario hubiera sido más prudente, precisamente por conocerse dicha debilidad.
Si resulta que al final el sistema "Nuevo" es vulnerable a "X", es decir, tal y como lo era el sistema "Antiguo", probablemente tendremos una situación "delicada"... tan delicada como un airbag que no funcione en el momento oportuno.
Para poner un escenario real, imaginemos un usuario utilizando su sistema de banca on-line con tarjeta de coordenadas desde un lugar público. Con los sistemas de contraseña estática, uno es consciente del riesgo que corre. Sin embargo con el sistema de coordenadas, aparentemente el riesgo es menor, y de hecho debería ser así. En este sentido, el usuario puede tomarse ciertas "licencias", asumir ciertos riesgos amparándose siempre en el hecho de que la probabilidad de que le "toque" un ordenador donde un desaprensivo se dedique a obtener contraseñas es pequeña, pero en el peor de los casos, obtendría solo una de las 60 contraseñas... y que justamente esa sea la que le pida el sistema al atacante en su posterior intento de fraude... sería muy mala suerte.
Ejemplos de ataques. Casos prácticos representativos.
Partiendo de las siguientes premisas:
- la tarjeta de coordenadas se compone de un conjunto de "N" contraseñas
- para cada transacción / operación el banco solicita una contraseña de dicha tarjeta
Se podría llegar a la siguiente conclusión:
- la captura por parte de un intruso de una sola contraseña de esa tarjeta no es garantía de éxito en un ataque, pues solo conoce UNA contraseña del total "N".
Esta afirmación puede inducir a error. De hecho, conceptualmente, y sin un análisis de la aplicación práctica del modelo teórico, podría llegar a parecer cierto, pero la realidad es que tanto esta afirmación, como muchas otras que se derivan de los modelos teóricos de muchas medidas de seguridad, pierden su validez en un entorno real, es decir, una vez se materializan en forma de código, como un programa que intenta reflejar dicho modelo.
Para el caso que nos ocupa, se ha detectado que la gran mayoría de implementaciones de los modelos teóricos correspondientes a las tarjetas de coordenadas presentan pequeñas, a veces imperceptibles, fallas que si bien no afectan en absoluto a la funcionalidad de la aplicación, si que ponen en riesgo o incluso pueden llegar anular la funcionalidad -en cuanto a seguridad se refiere- de estos sistemas.
Durante el estudio que PENTEST llevó a cabo sobre distintas implementaciones de los sistemas basados en tarjetas de coordenadas se detectó que en mayor o menor medida, prácticamente en todos los casos analizados existen particularidades de cada implementación que derivan en sistemas susceptibles de ser atacados con una probabilidad de éxito que en muchas ocasiones es cercano al 100%.
Supongamos los siguientes escenarios:
Escenario A: El sistema bancario solicita, para cada INTENTO de transacción, la clave correspondiente a una coordenada aleatoria de la tarjeta, y
sin importar si la transacción se ha concluido o no.
Este escenario es realmente peligroso. Una vez que el atacante tiene UNA contraseña perteneciente a la tarjeta de coordenadas, puede llevar a cabo un ataque basado en simular transacciones desde la cuenta de la víctima, pero sin llegar a confirmar o finalizar ninguna... Es decir el atacante comienza el proceso para realizar la transacción que desea, y cuando el sistema le pide la coordenada, si ésta coincide con la "suya" -la que ha capturado a la víctima-, la introduce y completa el ataque, si no, sale del formulario y vuelve a realizar todo el proceso de nuevo, entonces el sistema le pide la contraseña correspondiente a OTRA coordenada, si ésta es la que él posee la introduce, si no abandona el formulario y repite el proceso, tantas veces como sea necesario hasta que el sistema le pida la coordenada correspondiente a la contraseña capturada. Es cuestión de tiempo como puede demostrarse formalmente:
Si "N" es el número de claves de la tarjeta de coordenadas, tenemos que la Variable aleatoria que cuenta el número de intentos que se necesitan hasta que el sistema solicita la coordenada que tenemos sigue una distribución geométrica, luego:
P(X=n) = p(1-p)n-1, P(X<=n) = 1 – [1-p]n y E[X]= 1/p
Como en este caso tenemos que p=1/N el número esperado de intentos que hay que hacer es E[X]=1/(1/N)=N.
Si supondremos que el Número de coordenadas es 60, que una persona, manualmente, puede hacer una petición de transacción distinta cada 30 segundos y que mediante un programa que automatice el proceso podría hacer una por segundo, por ejemplo se tiene la siguiente tabla:
TABLA A
Como puede observarse el ataque tiene el éxito asegurado. En las pruebas que PENTEST ha realizado y sin necesidad de automatizar el ataque se han obtenido resultados positivos en pocos minutos, es decir, el ataque ha tenido éxito.
Otra forma de plantear el problema sería teniendo en cuenta la cantidad de veces que se quiere acertar imaginemos que "N" es el número de claves de la tarjeta de coordenadas, tenemos que la Variable aleatoria que cuenta el número de veces que el sistema solicita la coordenada que tenemos después de n intentos sigue una distribución Binomial, luego:
P(X=k) = [n!/k!(n-k)!](1-p)kp n-k
E[X]= np
Como en este caso tenemos que p=1/N el número esperado de veces que aparece la coordenada que tenemos para n intentos es
E[X]=1/(1/N)=n/N
Si suponemos que N es 60 obtenemos los siguientes éxitos esperados según el número de intentos que hagamos.
TABLA B
Nota: hay que tener especial cuidado con el mecanismo empleado para la solicitud de coordenadas. Algunos sistemas "parece" que siempre piden la misma coordenada para una transacción, aunque se abandone el formulario, sin embargo, si se desconecta la sesión, y se inicia una nueva, la coordenada varía. Si se quiere utilizar una coordenada fija para cada nueva transacción, hay que procurar que exista un sistema de seguimiento de las operaciones del usuario, FUERA del frontal bancario y que permita establecer cuando se puede pedir una nueva coordenada.
Escenario B:
Imaginemos el "Escenario A", pero un sistema que SI que pide siempre la misma coordenada para una nueva transacción, y hasta que ésta no finaliza, no pide una coordenada nueva. En este caso, el ataque es IDÉNTICO al anterior, con la salvedad de que el atacante debe esperar a que la "víctima" realice una transacción válida, para poder continuar con su ataque.
Como estamos partiendo del supuesto de que el atacante tiene acceso a la sesión del usuario (capturó usuario y contraseña) puede "monitorizar" cuando éste realiza una transacción. El ataque se basa en "inyectar intentos" entre transacciones válidas.
En este caso el éxito del ataque depende de la frecuencia con la que la víctima realice transacciones, de manera que las grandes cuentas, probablemente sean más vulnerables.
Supondremos un ataque automatizado, aunque en este ejemplo no tiene efecto en la velocidad, simplemente nos garantiza que una víctima nunca será más rápida que el atacante realizando una operación, y por lo tanto no se perderán intentos.
Basándonos en la tabla anterior,
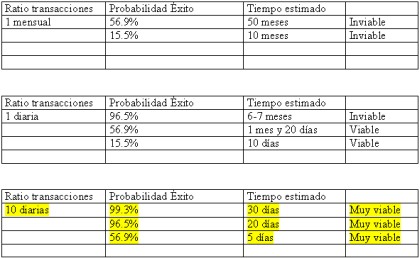Escenario C:
Supongamos ahora el "Escenario B" pero el sistema objeto de análisis utiliza un mecanismo OOB (Out of Band) para transmitir la coordenada que le solicita a su cliente.
Un sistema OOB, es un mecanismo para enviar credenciales u otra información por un canal alternativo, por ejemplo, vía SMS.
Aparentemente si el atacante no puede ver las coordenadas, no existe peligro. Sin embargo, no es necesario conocer la coordenada...
El ataque es idéntico al caso anterior. El atacante no necesita conocer la coordenada, simplemente "inyecta" su clave entre transacciones válidas. Si acierta, ya está, le es indiferente conocer a que coordenada pertenecía esa clave. De manera que son de aplicación las tablas anteriores.
Escenario D:
Supongamos el "Escenario A" pero con un sistema OOB para transmitir la coordenada. Este caso tiene la particularidad de que aun siendo vulnerable la lógica del programa, no se puede explotar tal y como se hacía en dicho escenario. La causa es que como el atacante no puede ver la coordenada, no puede "simular" transacciones no válidas y anularlas si la coordenada no le interesa. Debe llevar a cabo un ataque a ciegas, igual que en los escenarios "C" y "B", con el atractivo de que ahora dispone de 2 intentos antes de bloquear la cuenta, y por lo tanto el tiempo de ataque se reduce a la mitad. De manera que las tablas quedarían así (mostramos las dos más representativas):
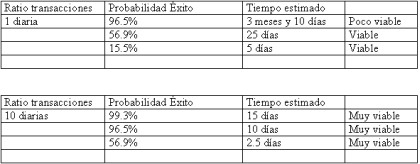ATAQUES COMBINADOS (ATAQUES EN PARALELO)
Este tipo de ataques son los más peligrosos de todos cuantos hemos podido estudiar. El objetivo de un ataque de este tipo es aumentar las probabilidades de tener éxito a base de aumentar el número de "victimas". Para ello, el intruso esperaría a obtener las credenciales de un buen grupo de usuarios de banca, y después montaría un ataque en paralelo contra todos los usuarios. Las posibilidades de este vector son increíbles, al tratarse de experimentos independientes la probabilidad de los mismos también lo son, luego la probabilidad de éxito será directamente proporcional al número de victimas que haya. Cada una de las victimas suma la misma probabilidad que un nuevo intento.
Si "N" es el número de claves de la tarjeta de coordenadas, tenemos que, al igual que en el caso anterior, la Variable aleatoria que cuenta el número de intentos que se necesitan hasta que el sistema solicita la coordenada que tenemos sigue una distribución geométrica, luego:
P(X=n,k) = p(1-p)n+k-1, P(X<=n) = 1 – [1-p]n+k
Traducido a cifras (tarjeta de 60 claves):
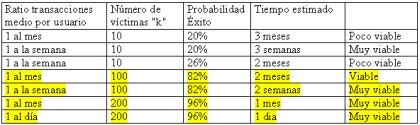
Este último tipo de ataques tiene una circunstancia agravante añadida, y es que aunque pueden detenerse, suponen un impacto importante en la clientela del banco. Imaginemos que un atacante ha conseguido credenciales de 100 usuarios. Comienza un ataque combinado en paralelo. Suponiendo que el sistema de la banca monitorizara los intentos de transacciones que quedan a medias, es decir sin finalizar -atención que esto es muy distinto de monitorizar fallos- se tendrían 100 cuentas de clientes con posibilidad de estar siendo atacadas. La única manera de detener esto es forzando a los usuario a cambiar sus claves... las de los 100 usuarios. Si el ataque se realiza sobre un número mayor de clientes, el impacto es importante.
ATAQUES COMBINADOS GENÉRICOS A CIERTOS SISTEMAS OTP
En general, uno de los eslabones débiles de los sistemas de validación por tarjetas de coordenadas, es el reducido número de claves posibles. En este sentido, es posible montar ataques combinados genéricos basados en intentos paralelos a distintas víctimas.
Para ello, vamos a emplear la situación más desfavorable de todas y a analizar que posibilidades de éxito tendría un ataque en este escenario.
Caso particular: ataque a un sistema de tarjeta de coordenadas con funcionalidad OTP (no reutiliza contraseñas) y que no permite repetición de claves dentro de la misma tarjeta.
En este escenario, el atacante se encuentra en una desagradable situación. Sin embargo, la particularidad de la "no-repetición de claves" dentro de la misma tarjeta, juega a su favor.
Siendo n= nº de intentos necesarios antes de obtener una de las claves que se tiene, k= nº de víctimas y N= nº de coordenadas, se tiene que la probabilidad de acertar la primera vez es:
P(X=n,k) = p(1-p)n+k-1, P(X<=n) = 1 – [1-p]n+k
Traducido a cifras tangibles:
Siendo N= 9999 (número de claves), y n= 59 (número de intentos)*
*Nota: se supone que si el sistema es OTP, las tarjetas se debe cambiar una vez agotadas las claves.
**Nota: suponemos un escenario ideal, en el que todas las víctimas tienen su "contador" de claves utilizadas a 0.
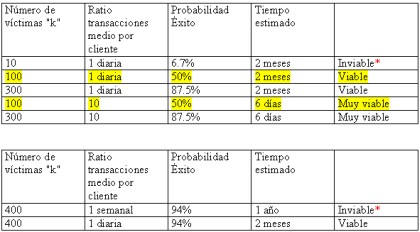
Como puede observarse, lo que determina la Probabilidad de éxito es el número de víctimas a las que se ataca en paralelo y lo que determina el tiempo empleado en el ataque es el Ratio de transacciones medio por cliente, que determina a su vez el ratio de "inyección" de intentos de acceso. Estas tablas están basadas en un conjunto de 59 intentos, es decir, las claves que tiene usualmente una tarjeta. A veces puede ser interesante para un atacante escoger modelos que si bien tienen menos probabilidades de éxito, son más veloces. Es decir la viabilidad viene definida -en principio- por la relación de los dos factores "Tiempo estimado" y "Probabilidad de éxito". La probabilidad de éxito no es lineal, sino que aumenta exponencialmente con el número de víctimas.
*Se debe tener cuidado en las valoraciones de lo que "es viable" y lo que no lo es.
En muchas ocasiones -en la gran mayoría-, factores externos influyen decisivamente a la hora de escoger un método de ataque.
Si observamos la tabla, veremos que la primera de todas las opciones:
Parece que un 6.7% de éxito puede no ser un aliciente para intentar un ataque que dure 2 meses. O puede que si... Si tenemos en cuenta que el atacante necesita de un tiempo determinado para recolectar datos de sus víctimas, podría ser "rentable" llevar a cabo un ataque de este tipo antes que esperar a tener "100" perfiles de victimas que realicen UNA operación al día!
Por otro lado, observemos este caso:
Puede parecer igualmente inviable. ¿Que atacante desea esperar un año? No parece merecer la pena. Sin embargo, habría que estudiar los casos intermedios de esta función.
Puede que la probabilidad de éxito en 2 meses sean lo suficientemente interesantes como para iniciar un ataque. Habría que estudiarlo.
Para tener una noción exacta de cual es la situación idónea para comenzar un ataque, se deberían tener por lo tanto en cuenta, como mínimo los siguientes factores:
- datos relativos a la distribución del ratio de operaciones medio por cliente. Este dato solo lo conoce con exactitud el banco, aunque puede determinarse mediante un estudio de campo.
- tiempo estimado en la recolección de datos de las víctimas. ¿Es el flujo de datos de víctimas constante o cada vez "cuesta más"?
- Tiempo de respuesta de los sistemas IDS del cliente. Fiabilidad de dichos IDS. En ese sentido: ratio de fallos generales y por usuario que hacen saltar las alarmas. Este dato no debería conocerlo el atacante, aunque puede realizarse un estudio de campo.
Por supuesto, existen otros ataques más complejos e igualmente interesantes basados en generar "colisiones", aprovechando la teoría de "Estimación del total de población de peces en un lago" descrita por Zoe Emily Schnabel en la American Mathematical Monthly en 1938. Popularmente se conoce esta teoría como la "Paradoja del cumpleaños".
Estos ataques se salen del objetivo de este borrador.
BREVES CONCLUSIONES
Una vez más, a falta de un estándar en cuanto a la implementación de un sistema de validación, se hace muy difícil generalizar para todos los casos.
Un sistema de autentificación basado en Tarjeta de Coordenadas puede implementarse de muchas maneras. Si bien no es el objeto de este documento establecer, cual es la manera correcta de implementar dicho sistema, si que parece interesante poner de manifiesto algunos puntos.
- La
longitud de las claves (PIN) , es decisiva a la hora de proteger el sistema de ataques directos al sistema de validación, el de la tarjeta de coordenadas y cualquier otro. Independientemente de la lógica del sistema de seguridad, requerir al usuario que se valide mediante una clave que tiene solo 9999 combinaciones posibles, es a todas luces insuficiente. Esto, independientemente de que exista un mecanismo de bloqueo de 3 fallos consecutivos o similar. El espacio muestral es demasiado pequeño y permite ataques "combinados" contra múltiples clientes.
-La decisión de si las
coordenadas deben cambiar o no a cada nueva transacción, depende del mecanismo empleado. En teoría parece más seguro forzar la petición de la misma coordenada para una nueva transacción -por lo visto en el "Escenario A"-. En general somos de esa opinión. En cualquier caso, esta opción tiene un efecto colateral que pocas veces se tiene en cuenta: el atacante puede conocer cual será la coordenada que se le va a solicitar a la víctima. Para poner un ejemplo de como puede ser explotada esta debilidad, imaginemos que un intruso consigue monitorizar los usuarios y contraseñas de distintos clientes, por ejemplo en un ordenador público. Desgraciadamente para el atacante, el sistema que utilizan el banco de esos clientes es OTP, no reutiliza claves y fuerza la introducción de la clave correspondiente a una coordenada determinada para una nueva transacción. Bien, en este caso, el atacante puede llevar a cabo un vulgar intento de phishing para obtener en cada caso, la coordenada que necesita de cada cliente. ¿Cómo? Simplemente debe esperar a tener el suficiente número de credenciales de acceso de sus víctimas, para luego intentar una transferencia a fin de asociar a cada cliente la "siguiente" coordenada que se solicita. Acto seguido el intruso debería llevar a cabo un ataque de phishing "personalizado", solicitando a cada víctima, la coordenada que necesita. Es un sistema mucho más "fino" que lo que actualmente realizan algunos atacantes que solicitan introducir todas las coordenadas de la tarjeta... realmente tosco.
La excusa perfecta para el atacante es la necesidad de "identificar" al cliente. Las opciones son infinitas. Por ejemplo, en un ataque de ingeniería social, alguien puede argumentar: "No le solicitamos su usuario y contraseña de acceso señora -por que ya lo tenemos- eso no debería usted dárselo nunca a nadie, pero necesitamos identificarla. Por favor díganos cual es el PIN correspondiente a la coordenada X". Si se paran a pensarlo, verán que es un vector de ataque muy interesante. Para un informático o entendido en la materia, el ataque está claro. Pero en este caso, la manipulación de la víctima que se puede llevar a cabo es importante.
- Puede considerarse que un buen sistema de prevención de intrusos permite identificar todo este tipo de ataques, pero quizá debería tenerse en cuenta que si bien es una herramienta interesante, e imprescindible hoy en día, el bypass de este tipo de sistemas no suele ser tarea imposible. Veamos un ejemplo. Supongamos que el sistema de banca tiene un mecanismo de detección de intentos fallidos de introducción de claves de la tarjeta de coordenadas. Supongamos también, que el sistema lleva a cabo un análisis estadístico, por ejemplo para descubrir si una serie de eventos siguen una distribución de Poisson, es decir para ver si estos eventos son fruto del azar o no, de manera que si se producen distintos fallos secuenciales como consecuencia de un ataque, probablemente salten las alarmas. Incluso en ese caso, se puede montar un ataque muy simple que simule eventos aleatorios simplemente ajustándose a dicha distribución.
Como resumen de este Anexo, se debería recordar que en función de los escenarios, tenemos que:
Como puede deducir el lector interesado en esta problemática, este texto es solo una vista de pájaro, genérica, sobre los sistemas de autentificación basados en Tarjetas de Coordenadas. De igual modo, queremos pedir disculpas por adelantado por los posibles errores de cálculo que puedan existir. Debe tenerse muy en cuenta que la mayoría de casos planteados se resuelven a partir de modelos teóricos, y casos ideales, que en muchas ocasiones no se ajustan a la realidad de cada cliente y de cada implementación en concreto.
AGRADECIMIENTOS
Queremos agradecer sinceramente la colaboración de distintas Cajas y Bancos de toda España por la sensibilidad mostrada ante este estudio, en especial a la C.E.C.A. (Confederación Española de Cajas de Ahorro), BBVA y La Caixa -entre otros-
Agradecimientos a David Villanueva Jiménez (Artica S.L.), por la revisión de los cálculos matemáticos.
ÚLTIMAS ACLARACIONES
A pesar de nuestros esfuerzos, el hacer llegar éste informe a
todas las entidades ha sido tarea imposible. Aun así gran parte del sector ha sido informado. En cualquier caso,
PenTest estará a disposición de cualquier entidad financiera que se acredite como tal para informarla y sin compromiso alguno.
http://www.pentest.es
info@pentest.es
933 962 070
Los clientes de banca electrónica
NO DEBEN ALARMARSE por éste informe, pues el interés del mismo radica principalmente en la base teórica en que se fundamentan los ataques aquí descritos y no en la probabilidad real de que hoy en dia alguien los ponga en práctica.
Excepto casos aislados, la respuesta de la banca ha sido muy buena. La seguridad de la banca online si bien no es perfecta
no puede considerarse inferior a la de cualquier otro negocio on-line, muy al contrario es superior en casi todos los aspectos.
El miedo nunca ha sido buen aliado del progreso, y en ese sentido tenerle miedo a la banca electrónica, NO está justificado, siempre y cuando el nivel de "ciber-delincuencia" no alcance límites insostenibles. Hágase una pregunta: ¿A cuantas personas conoce que hayan sido víctimas de un robo online? Ojo, no se trata de relajarse. Es muy recomendable revisar estos sistemas periodicamente, simulando situaciones extremas, pues aunque el exceso de paranoia nunca fue saludable la carencia absoluta de la misma no nos proporcionará más seguridad.
Mas información:
Hugo Vázquez Caramés
(Director Técnico de PENTEST, Consultores de Seguridad Telemática)
http://www.pentest.org
Nota: B.E.S.T. (Banca Electrónica Seguridad Telemática), orientado precisamente a Tests de Intrusión y consultoría en sistemas de Banca Online. A parte de las pruebas de auditoría, en PenTest hemos desarrollado distintas mejoras para los sistemas de autentificación que anulan la inmensa mayoría de los ataques descritos tanto en el informe inicial como en el anexo así como otros más complejos. Algunos bancos de fuera de nuestras fronteras ya se han interesado por nuestras soluciones.
"PenTest expresamente acepta la cesión de los derechos de publicación de este informe a favor de la Asociación de Internautas".
